サーミスタで温度を計る

　他の頁でサーミスタの抵抗値の温度変化に関する公式とメーカーの公表値の違いを検証してみました。
　具体的な温度計測に関しては記述してなかったので、追加する予定だったのですが、当該ページのタイトルと合わなくなるので、 新しいページとしました。
　今回は気温ということで−１０℃〜４０℃の範囲の温度を計る事にします。
　サーミスタで温度を計る時に精度を上げるには計測範囲を広くとらないことが重要です。
　計測スパンを５０℃にすれば簡単なソフトハードで±１℃の精度で計測可能です。
　ＩＣ温度センサーは高精度で計れるイメージがありますが、±２℃とか±３℃とか書かれているものが多いです。

　サーミスタの選択

　サーミスタにも色々な種類があります。
　いずれも温度変化に対する抵抗値の変化を利用するのですが、今回のように温度を計測する用途だけとは限りません。
　昔はゲルマニュームトランジスタのバイアスの温度補正をするために使ったりしました。
　温度を計測するには高精度の計測用サーミスタを使います。
　今回はセミテックの１０３ＡＴ−１１を使いました。
　計測用サーミスタとしては入手が楽なものです。



　長さ１５ｍｍ（リード線を除く）φ５位の円筒形です。
　写真の様にセンサーとして使い易い形状をしています。
　ただし、１０３ＡＴには他に４種類位の形状があり、１０３ＡＴ−２とか１０３ＡＴ−３とかの名称が付いています。
　１０３の数字の意味は２５℃の抵抗値が１０ＫΩであることを示しています。
　例えば５ＫΩのものは５０２ＡＴとなります。
　１０ＫΩのものが最も一般的に使われているような気がします。
　応答性は、それ程良くはありませんが、気温を計るには使い易い物です。



　セミテックの計測サーミスタはＡＴシリーズだけではありません。
　上の写真は１０３ＥＴです。
　非常に小型で胡麻粒より小さいです。
　小さすぎて、やや、取り扱いが面倒です。
　特徴は小型の為、応答性が良く、被測定物体に影響を与えないことがあります。
　反面、許容損失が小さく、使用電圧を下げないと自己発熱の影響を受けます。
　ここでは使いませんが、他のページ「部品の温度を計る」で使用しています。
　ＡＴ、ＥＴ以外にも多くの種類があります。

　温度−抵抗値変換テーブルを用意する

　他のページで述べたようにサーミスタのＢ定数を使って温度から抵抗値を求めることが出来ます。
　逆に抵抗値から計算により温度を求めることが可能な筈です。
　しかしながら、性能の低いマイコンでは重い負荷となります。
　従って、予め、温度に対する抵抗値の換算表を用意しておきます。
　換算表があればテーブル引きをしてもよいのですが、テーブル引きも、そこそこメモリを使います。
　温度と抵抗値の関係が直線近似出来れば簡単な計算で温度を求める事が出来ます。
　温度と抵抗値の変換テーブルはセミテックのホームページで入手出来ます。
　Ｂ定数を使って計算で求める事も出来ますが、０℃以下で誤差が大きくなります。
　セミテックがホームページで公表している変換テーブルは１０℃ステップのものです。
　（Ｂ定数に関係している２５℃と８５℃のデータはあります。）
　欲を言えば５℃ステップのデータが欲しいので、仕事で使う場合などでは要求すれば貰えるかもしれません。
　（昔は５℃ステップのデータが公表されていたと思います。）

　直列抵抗でリニアライズ

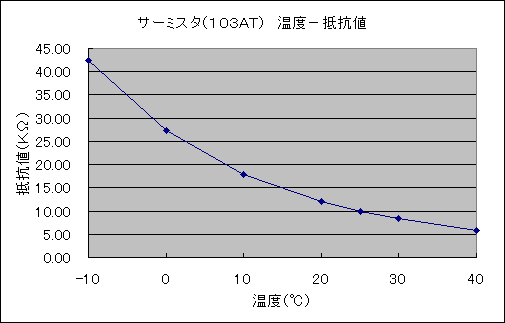
　上のグラフは１０３ＡＴの温度と抵抗値の関係です。
　指数関数になっていますので、このままでは大変です。
　また、直接、抵抗値は測定出来ないのでサーミスタに加わる電圧を計測して温度と電圧の関係式を求めます。
　サーミスタと直列抵抗を基準電圧に接続し、分圧された電圧と温度の関係を見ると直線に大きく近づきます。
　さらに近似直線を求めると計測電圧から簡単に温度が計算できます。

計測回路

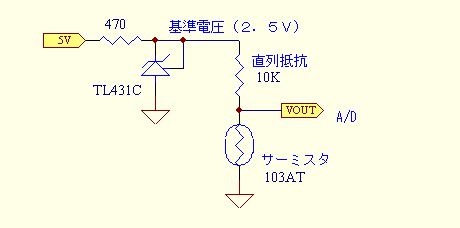
　上に計測回路を示します。

　基準電圧
　この基準電圧はＡ／Ｄ変換器の基準電圧とは別ですが兼用することも出来ます。
　温度の変化や温度変化による負荷の変動に対し、安定である必要がああります。
　回路図では電圧源にＴＬ４３１を使っていますが他でも構いません。
　電圧は何でも構わないのですが、値を正確に知っておく必要があります。
　応答が早い小型のサーミスタは許容損失が小さく、電圧を下げないと自己発熱で温度が上がります。
　１０３ＡＴの場合、５Ｖでも大丈夫ですが１０３ＥＴを５Ｖで使うと自己発熱の影響を受けます。
　電圧が１／２になれば損失は１／４になるので２．５Ｖでは大丈夫と思います。
　専門書を見ればサーミスタのデータから自己発熱による温度上昇の値が計算できるはずです。

　直列抵抗の値
　回路図は１０ＫΩを使っていますが多少、値がずれても構いません。
　ただし、正確な値を知っておく必要があります。
　１０ＫΩという値ですが計測スパンの中間位の温度におけるサーミスタの抵抗値を使えば誤差を少なく出来ます。
　仮に計測スパンが０℃〜５０℃とすれば中間値は２５℃となり、１０３ＡＴの抵抗値は１０ＫΩとなります。
　今回は−１０℃〜４０℃ですので１０ＫΩより少し大きい値が最適値となるはずです。
　専門書を見れば直列抵抗の最適値は計算で求まると思いますが、エクセルでカットアンドトライする方法があるので 後で紹介します。
　直列抵抗自体は温度変化が少ない方が良いので金属被膜抵抗を使います。

　エクセルで近似直線の方程式を得る

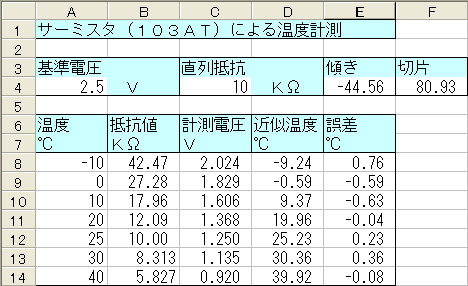
　上の表で基準電圧と直列抵抗は変数を入力するセルを用意して入力します。
　キッチリした値で無くても良いですが、正確な値を入力します。
　温度と抵抗値はメーカー提供の換算表そのものです。
　計測電圧は基準電圧を直列抵抗とサーミスタで分圧した計算値ですが、実際に計測しても、この値になるはずです。
　−１０℃に於ける計算式を例に挙げると。
　Ｃ８＝＄Ａ＄４＊Ｂ８／（Ｂ８＋＄Ｃ＄４）
　となります。
　これで温度と計測電圧の関係をを直線近似した方程式が求められます。
　直線の方程式には傾きと切片がありますが、これらをエクセルの関数で求めます。
　温度をＴ、電圧をＶとし、傾きをＡ、切片をＢとします。
　Ｔ＝ＡＶ＋Ｂの近似式を求めてみます。
　傾きと切片は同時には求まらず、別々に求めます。
　それぞれ、結果を収納するセルを用意し、選択した状態で関数を挿入します。
　傾きを求める関数名はＳＬＯＰＥ、切片を求める関数名はＩＮＴＥＲＣＥＰＴです。
　関数が呼ばれたら、まずＹ軸の範囲（Ａ８〜Ａ１４）を選択し、次にＸ軸の範囲（Ｃ８〜Ｃ１４）を選択します。
　これで用意したセルに数値が入ります。
　近似温度は計測電圧と近似直線から求めた温度です。
　例えば−９．２４℃の位置の計算式は
　Ｄ８＝Ｃ８＊＄Ｅ＄４＋＄Ｆ＄４
　となります。
　誤差は正しい温度と計算で求めた温度の差を示します。
　±１℃以内に収まっています。

　近似直線の求め方を変えてみる

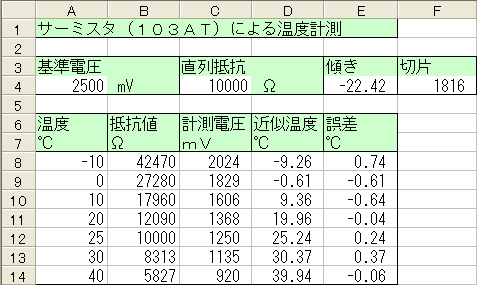
　前項で計測電圧から温度が簡単に求まりました。
　ただし小数点の計算となってしまいます。
　出来るだけ整数計算で済ませたいものです。
　上の表は計算方法とスケーリングを変えたものです。
　まず、電圧はｍＶ単位、抵抗はＫΩではなくΩで入力します。
　次にＸ軸とＹ軸を入れ替えてみます。
　前回はＹ軸が温度、Ｘ軸が電圧でしたが今回はＹ軸が電圧、Ｘ軸が温度となります。
　Ｘ軸が温度の方がグラフが見易いということもあります。
　温度をＴ、計測電圧をＶ、傾きをＡ、切片をＢとすると
　Ｖ＝ＡＴ＋Ｂ
　Ｔ＝（Ｖ−Ｂ）／Ａ
　となり、一手間増えるようですが結果的にはこちらの方が楽でした。
　傾きと切片を求める時、ＸとＹの選択が逆になります。
　当然ながら前項で求めた傾きと切片とは全く別の値になります。
　例として表で−１０℃に対応する−９．２６℃のところの計算式は
　Ｄ８＝（Ｃ８−＄Ｆ＄４）／＄Ｅ＄４
　となります。
　具体的な数値を入れると
　求める温度　＝（２０２４−１８１６）／２２．４２
　となります。
　マイコンでの計算では分母分子を１００倍して
　（２０２４００−１８１６００）／２２４２とします。
　このままでは小数点以下は切り捨てられてしまうので、必要に応じ、さらに分母に１０又は１００を掛けます。
　１００を掛ければ小数点以下２桁の数値が１００倍の整数として扱えます。
　尚、余りを切り捨てるのではなく、四捨五入したいときは被除数に除数の１／２を加えてから割り算します。
　いずれにせよ４バイト長（ｌｏｎｇ）の計算となります。

　直列抵抗を調整してみる

　直列抵抗には最適値があると言いましたが、この値をエクセルでカットアンドトライしてみます。
　表は直列抵抗に１１ＫΩを入力したものです。 　このセルは他のセルから相対参照されているので、グラフも含めた関係する全ての項目が一瞬で切り替わります。
　直列抵抗を１１Ｋにしたら誤差が小さくなりました。
　注意点として数値のみが入力されたセルは値を入力出来ますが、数式が入力されたセルに数値を手入力すると 数式が消されてしまうということがあります。
　例えば傾きを表示するセルに数値を手入力してはいけません。

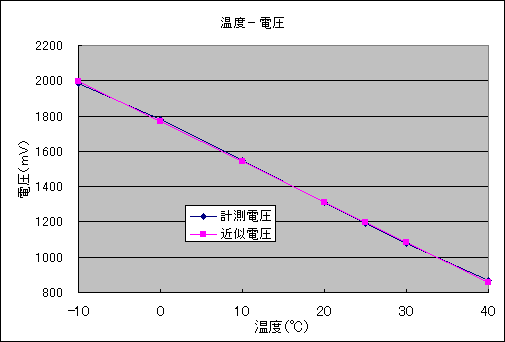
　直列抵抗１本でどれだけリニアライズされたかグラフに表示してみました。
　表に近似電圧という項目を追加しました。
　グラフで赤線が近似直線です。
　青線がリニアライズされた計測電圧です。
　殆ど直線に近い事が解ります。

　その他

　今回は計測スパンを−１０℃〜４０℃としました。
　温度が範囲外でも数値は出てきますが、精度は急激に悪化します。
　最初から計測スパンを広く取った場合、精度は悪くなります。