トップページ
電子回路のページのトップ
サーミスタの温度−抵抗変換式
サーミスタとIC温度センサー
 サーミスタ
サーミスタ
 IC温度センサー
IC温度センサー
気温レベルの温度を計測するにはIC温度センサーかサーミスタを使います。
シリコンダイオードもセンサーとして使えますが校正作業が必要となります。
低温や高温を測定するには熱電対や白金測温体を使いますが簡単に使えるものではありません。
手元にはサーミスタとIC温度センサーのストックがあるのですが、どうしてもサーミスタを使ってしまいます。
写真をみると判りますが、IC温度センサーは外形がトランジスタと同じで、基板に取り付けるには良いのですが、リード線で
外部に引き出すには向いていません。
その点、サーミスタはそのままセンサーとして外部に引き出せる形をしています。
そして、様々な大きさのものがあります。
写真の一番小さなものは胡麻粒より小さいです。
形状も色々なものが有り、センサー部がネジで固定できたりするものもあります。
サーミスタはリード線が2本であるのもメリットです。
IC温度センサーはリード線が3本ですので、複数のセンサーを外部に引き出す時は手間が増えます。
ICセンサーの中には出力端子に電源を重畳させて2本にしたものとか、バス状に芋蔓式に接続出来るものもあるようですが、
高価だったり、使うのが面倒だったりします。
一般的なIC温度センサーは意外と精度が悪く、写真のもので最大誤差は±3℃と規定されています。
高精度サーミスタを使えば±1℃程度で計れると思います。
IC温度センサーにも高精度のものがありますが、高価で、ゲジゲジICのパッケージだったりします。
温度−抵抗値変換テーブル
サーミスタの抵抗値から温度を求めるには変換テーブルを使い、関係を直線近似します。
サーミスタの抵抗値は電気的に求める事が出来ます。
例えば既知の抵抗を直列に接続し、分圧した電圧を測定します。
さて、温度に対する抵抗値の値はメーカーから発表されています。
私がよく使う103ATや103ETもメーカーサイトに掲載されています。
ところが以前メーカーから入手出来たデータは5℃ステップでしたが、最近は10℃ステップになっています。
25℃と85℃はデータがありますが、25℃の抵抗値を基準にしていることとB定数を25℃と85℃から求めている為と
思います。
直線近似するには全範囲5℃ステップ程度のデータが欲しいです。
サーミスタの抵抗値を計算する
B定数と温度からサーミスタの抵抗値を計算する式が存在します。
数式の記述をするのは面倒ですので秋月電子に参考資料としてアップされていたものをコピーさせて
頂きました。

この式を使えば任意の温度ステップで換算表が作成出来るはずです。
尚、この式を逆算すれば直接、抵抗値から温度が求められるはずですが、チープなマイコンでは負担が大きすぎるので、予め
換算表を作成して直線近似し、一次関数の解として温度を求めます。
エクセルの関数で計算してみる
上記の数式をエクセルの関数で記述すると
R=10*EXP(3380*(1/(50+273)-1/(25+273)))
=4.157 となります。
実際にはRは答えを出力するセルの相対位置、T(50℃)は温度を入力したセルの相対位置を示します。
25℃の抵抗値(10KΩ)やB定数(3380)は直接数値を入力しても良いですが、特定のセルに書いて絶対参照すれば
便利です。
この値を変えれば表全体が再計算されます。
103AT 温度−抵抗値換算表
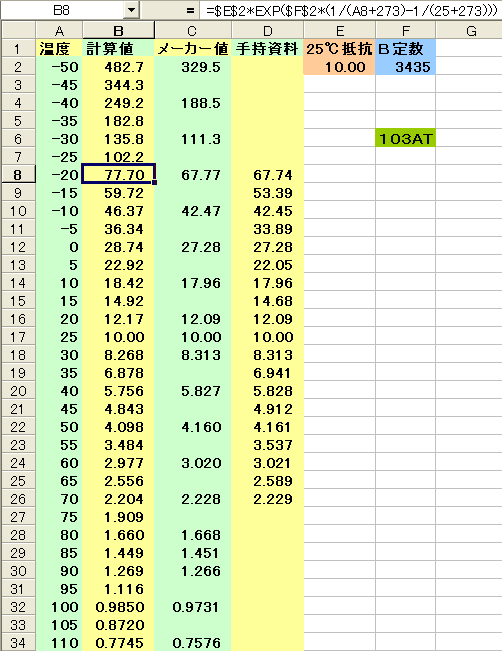
表は手持ちのサーミスタ103ATの温度に対する抵抗値の換算表です。
温度とB定数以外の数値は全て抵抗値で単位はKΩです。
計算値は前述の計算式で求めた値です。
計算式は−20℃のセルを選択して表示しています。
メーカー値は現在、製造元が公開している抵抗値で25℃と85℃以外は10℃ステップです。
手持ち資料は以前、103ATの換算値として私が使用していたもので、若干の誤差がありますが、ほぼメーカー値と同じ
です。
多分、以前はメーカーから5℃ステップの値が公開されていたものと思われます。
ひょっとしたら誰かが恒温槽で実測したのかもしれませんが。
計算値とメーカー値は特に低温側で大きな差があります。
データをグラフにしてみました。
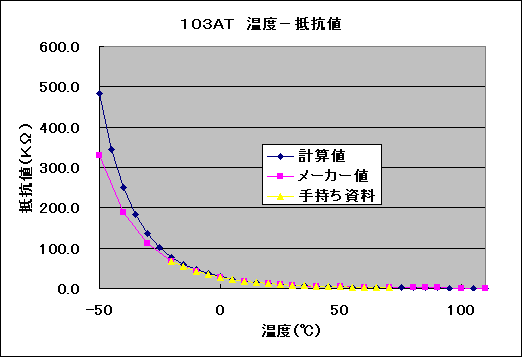
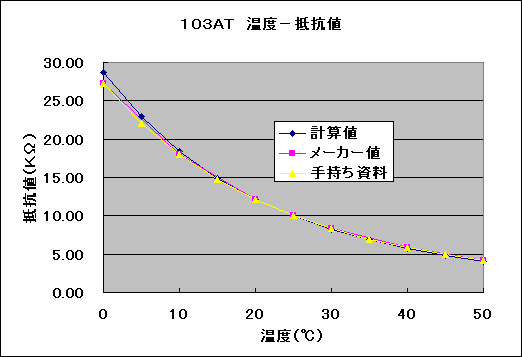
低温側では大きな違いがありますが、範囲を0℃〜50℃に絞ると差は縮まります。
103ET 温度−抵抗値換算表

103ETに関しても計算値とメーカー値を比較してみました。
103ETのメーカー値は大部前にメーカーから取り寄せた5℃ステップのものを入力してあります。
この値は現在、メーカーのサイトから得られる値と完全に一致します。
ただし、現在、公開されているデータは10℃ステップです。
計算値とメーカー値は、やはり低温側の差が大きくなります。
全範囲と0℃〜50℃の範囲のデータをグラフ表示してみました。
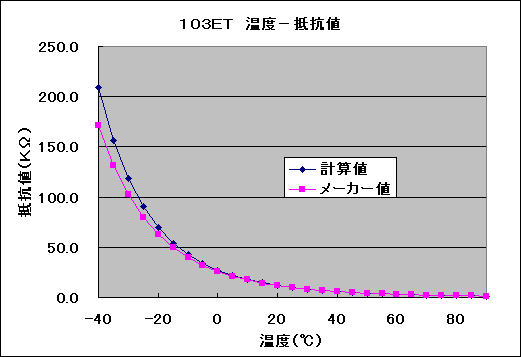

サーミスタの抵抗値を計算してくれるサイト
サーミスタの抵抗値を高精度で計算してくれるサイトを発見しました。
入力項目は温度の上限値と下限値、基準温度(25℃)、基準抵抗値(25℃での抵抗値)、B定数(メーカー公表値)、
表示ステップ(5℃を入力)です。
以上の項目を入力すると温度−抵抗値の表を出力してくれます。
秋月の計算式と同じものを使っているので、上記計算値に近い値を出力します。
僅かな誤差がありますが、計算途中の数値の丸め方や演算精度の違いと思われます。
やはり、メーカーの抵抗値とは誤差以上の差があります。
結論として
サーミスタのB定数から抵抗値を求める公式は一般的に認知された式ですので誤りではありませんが、実際のサーミスタの
抵抗値とは、特に低温側で差があるようです。
B定数は25℃と85℃の2点の抵抗値から一般的には求められるようですので、この範囲では比較的、計算値と実際の値が
合っています。
85℃以上は使用範囲の残りが少ないので、あまり問題がありません。
25℃以下では少しずつ誤差が増えはじめ、0℃あたりになると結構、差が目立ちます。
寒冷地で−10℃の気温を計る場合、要求される精度によっては問題があると思われます。
この場合はメーカーで公表している値を使用した方が良いと思います。
請求すれば5℃ステップのデータを頂けるかもしれません。(保証はしませんが。)
B定数の説明をしているサイトによるとB定数は完全な定数ではなく、条件によって変動する値と記されていました。
トップページ 「電子回路」のトップ


 サーミスタ
サーミスタ IC温度センサー
IC温度センサー



